CIU Matemático: TEORIA DE CONJUNTOS

Idea de conjunto

Todos tenemos la idea de lo que es un conjunto: es una colección, agrupación, asociación, reunión, unión de integrantes homogéneos o heterogéneos, de posibilidades reales o abstractas. Los integrantes pueden ser números, letras, días de la semana, alumnos, países, astros, continentes, etc. a estos integrantes en general, se les denomina "elementos del conjunto".

Ejemplos:

a) El conjunto formado por los primeros veinte números naturales.
b) El conjunto formado por docentes de una Institución Educativa.
c) El conjunto formado por los actuales presidentes regionales del Perú.
d) El conjunto formado por las computadoras de una cabina de Internet.

Sin embargo, el concepto que tenemos es un "concepto intuitivo", el cual pues no es correcto pues también existe conjuntos formados por un solo elemento y conjuntos formados sin elementos lo cual contradice la idea que teníamos.

Ejemplos:

a) El conjunto constituido por los animales que maman.
b) El conjunto de ciudades de la sierra peruana.
c) El conjunto de los números naturales menores que 6 y mayores que 5.5
d) El conjunto de de personas mayores de 500 años de edad.

Definición tentativa de conjunto

Si tomamos todas las ideas anteriores entonces conjunto se define como "la presencia o ausencia de elementos con características semejantes dentro de un contexto real o imaginario".

NOTACIONES DE UN CONJUNTO

I. A conjuntos se les denotará con letras mayúsculas A, B, C…..y a sus elementos con letras minúsculas; a, b, c, d,…...para separar los elementos se emplean comas (,) y el punto y coma para separar conjuntos o subconjuntos.

Ejemplo:

II. El símbolo empleado para expresar que un elemento pertenece a un conjunto es: (

Ejemplo:

III. el símbolo utilizado para expresar que un elemento "no pertenece" a un conjunto es: (

Ejemplo:

IV. Cuando un conjunto "R" está constituido por varios elementos como por ejemplo: a, e, i, o, u o por subconjuntos: {2}; {3, 4}; los escribimos entre LLAVES "{}".

Ejemplo:

Determinación de conjuntos

1. Por Extensión

Un conjunto "D" está determinado por extensión cuando se mencionan uno por uno todos sus elementos o cuando, si son números, se mencionan los primeros de ellos (y se coloca puntos suspensivos)

Ejemplos:

D = {lunes, martes, miércoles, jueves, viernes, sábado,

domingo}

C = {0, 1, 2, 3, 4, 5,…………………}

Sin embargo, no todos los conjuntos pueden ser determinados de esta sobre todo cuando el número de elementos que constituyen el conjunto es muy elevado.

Imagine los casos de aquellos conjuntos que tienen infinitos elementos como el conjunto de estrellas del universo.

Es por ello, que necesariamente, se debe emplear otro procedimiento para determinar los conjuntos que tienen muchos elementos. A esta otra forma de determinar a un conjunto se le denomina comprensión que también se puede utilizar para cualquier conjunto.

2. Por Comprensión

Un conjunto "D" está determinado por comprensión cuando se enuncia una ley o una función que permite conocer que elementos la cumplen y por tanto, van a pertenecer al conjunto D.

Para diferenciar cada forma de determinar un conjunto veamos los siguientes ejemplos:

Ejemplo 1

Por extensión:

D = {lunes, martes, miércoles, jueves, viernes, sábado, domingo}

Por comprensión: (una posible respuesta sería)

D = {x/"x" es un día de la semana}

Se lee:

"El conjunto D está formado por todos los elementos "x" que satisfacen la condición de ser un día de la semana".

Otra posible respuesta sería:

"D es el conjunto constituido por todos los elementos "x" tal que X es un día de la semana"

Ejemplo 2

Por extensión:

C = {0, 1, 2, 3, 4, 5,…………………}

Por comprensión: (una posible respuesta sería)

C = {x/x = (2n – 1) ^ x(N}

Se lee:

"C es un conjunto formado por los elementos "x" tal que "x" es un número impar y "x" pertenece al conjunto de los números naturales.

Ejemplo 3

Determinar por comprensión el conjunto "S" formado por los elementos dos y tres.

Por extensión:

S = {2,3}

Por comprensión:

S = {x/x2 - 5x + 6 = 0}

Se lee.

"S es un conjunto formado por los elementos "x" tal que x al cuadrado menos cinco x mas seis es igual a cero.

Clases de conjuntos por el número de elementos

1. CONJUNTO UNITARIO

Es aquel conjunto que tiene un solo elemento.

Ejemplos:

2. CONJUNTO VACIO (O NULO)

Es aquel conjunto que no tiene elementos.

Ejemplo:

A = {es el conjunto de aves que tienen 3 patas}

B = {es el conjunto de hombres con 4 piernas}

Como se habrá dado cuenta no existe ninguna ave u hombre con tres patas o cuatro piernas respectivamente, por tanto, estos conjuntos carecen de elementos y decimos que es un conjunto VACIO.

Conjunto universal: (o universo)

Es el conjunto que contiene, comprende o dentro del cual están todos los demás conjuntos, se le simboliza por letra U, gráficamente se le representa mediante un rectángulo en cuyo vértice (uno cualquiera) se coloca la letra U.

Si consideramos como un conjunto universal al sistema Universitario de nuestro país, entonces cada Universidad x, será elemento de dicho universo. El conjunto de libros de una biblioteca determinada, puede ser otro ejemplo, sus elementos serán cada uno de los libros de los que consta. El marco de referencia es relativo, de modo que podemos referir como conjunto universal por ejemplo al conjunto de Bibliotecas de Contumazá.

4. CONJUNTO FINITO

Es aquel cuyos elementos se pueden contar en forma usual desde el primero hasta el último. El número de sus elementos se llama cardinal de conjunto.

Ejemplos:

5. CONJUNTO INFINITO

Si contamos no llegamos nunca a un último elemento del conjunto mencionado. A este tipo de enunciados se denominan conjuntos infinitos o indefinidos.

Ejemplo:

1. A = {1, 2, 3,……………..,100} (es finito)
2. B = {1, 2, 3,…………………….} (es infinito)
3. C = {……-4, -3, -2, -1, 0, 1, 2, 3, 4………} (es infinito)

Relaciones entre conjuntos

1. INCLUSIÓN

Se dice que "A" está incluido en el conjunto "B", cuando todo elemento de A, pertenece a "B". La inclusión se simboliza por: "("

También se puede decir que A es subconjunto del conjunto B. Se puede denotar por B(A, que se lee "B incluye, contiene al conjunto A"

Ejemplo:

Si: P = {vacas}

M = {mamíferos}

Entonces se tiene:

Sean por ejemplo los conjuntos:

A = {a, b, c, d} B = {a, d}

C = {b, d, a, c} D = {a, c, e}

En este caso se observa las siguientes inclusiones:

B ( A; C ( A; A ( C

En cambio los conjuntos "C" y "D" son incomparables, porque ni "C" incluye a "D", ni "D" incluye a "C", es decir:

D (C; C(D

Hemos visto que pueden ocurrir al mismo tiempo las dos inclusiones C ( A y A ( C, esto quiere decir, que A = C.

2. CONJUNTOS IGUALES

Dos conjuntos son iguales si tienen los mismos elementos, su forma simbólica es: A = B

Nótese que decimos los mismos elementos que no es igual a decir el mismo número de elementos.

De la definición podemos inferir que: A = A (todo conjunto es igual a sí mismo).

Ejemplo 01

Si: A = [1, 3, 7, 9, a, b} B = {a, b, 9, 3, 1, 7}

Entonces: A = B pues son los mismos elementos aunque estén en diferente orden. Recuerde, no importa el nombre dado al conjunto si no los elementos que lo forman.

Ejemplo 02

Si: C = {a, e, o, i, u} D = {a, e, o, 3, u}

Entonces: C?D porque a pesar de que cada conjunto tiene cinco elementos (igual número de elementos) basta que exista un elemento diferente para que ya no sean iguales.

3. CONJUNTOS DIFERENTES

Dos conjuntos son diferentes si sus elementos no son iguales.

Ejemplo:

4. CONJUNTOS DISJUNTOS

Dos conjuntos son disjuntos si no tienen ningún elemento en común: es decir, todos los elementos de un conjunto son diferentes a los elementos de otro conjunto.

Ejemplo:

A = {0, 1, 2, 3, 4, 5} B = {9, 8, 7, 6, 10}

En este caso podemos apreciar que ningún elemento de A o B son los mismos a esto se denomina conjuntos disjuntos.

5. CONJUNTO POTENCIA

Se llama así al conjunto formado por todos los subconjuntos que es posible formar de un conjunto dado. Se simboliza por P. La notación P(A), se lee: "potencia del conjunto A". El número de subconjuntos que es posible formar con los elementos de un conjunto es: 2n siendo "n" el número de elementos integrantes del conjunto dado.

Ejemplo:

Se pueden intuir muchos sistemas auxiliares para visualizar las relaciones; entre conjuntos, los más conocidos son los diagramas lineales y los de Venn-Euler.

1. DIAGRAMAS LINEALES

Son aquellos en donde se emplean líneas "(" para determinar la jerarquía entre conjuntos y se grafican uno debajo de otro teniendo en cuenta si es subconjunto o está incluido en el que va en la parte superior.

Ejemplo:

Si el conjunto universal lo forman las letras del alfabeto y además se tiene los siguientes conjuntos:

A = {a, b, c, d}

B = {c, a, d}

C = {a, d}

Observamos que : C ( B; además B ( A; y como U es el conjunto universal (todas las letras del alfabeto)

La representación lineal será:

2. DIAGRAMAS DE VENN-EULER

Consiste en graficar mediante círculos, elipses, rectángulos, u otras figuras geométricas de área plana, cada uno de los conjuntos con los que se labora. Generalmente los puntos interiores a un rectángulo representan al conjunto del sistema.

Ejemplo: (teniendo en cuenta el ejemplo anteriormente desarrollado en el caso de los diagramas lineales)

Si el conjunto universal lo forman las letras del alfabeto y además se tiene los siguientes conjuntos:

A = {a, b, c, d}

B = {c, a, d}

C = {a, d}

Observamos que : C ( B; además B ( A; y como U es el conjunto universal (todas las letras del alfabeto)

La representación de los diagramas de Venn-Euler:

Observamos que el conjunto C esta en el interior del conjunto que lo incluye del mismo modo, B respecto de A. el conjunto universal está representado por el rectángulo en nuestro ejemplo; que a su vez está formado por las letras del alfabeto.

C ( B ( A ( U

Operaciones entre conjuntos

Las operaciones entre conjuntos son las disposiciones específicas de combinar conjuntos para formar otros, de semejante estructura. Dichas operaciones son la unión, la intersección, la diferencia, la complementación, el conjunto Producto o conjunto cartesiano, y la diferencia simétrica.

1. UNIÓN O REUNIÓN

Unión o reunión de los conjuntos A y B es el conjunto de elementos "x" que pertenecen a "A", a "B" o a ambos, se simboliza por: A(B; y se lee: "A unión B"

Por comprensión:

Gráficamente, la unión de conjuntos se representa, en un diagrama de Venn-Euler, achurando la zona donde se encuentran los diversos elementos que pertenecen a los conjuntos que van a formar la unión o reunión.

Ejemplo:

PRO PIEDADES DE LA UNIÓN DE CONJUNTOS

2. INTERSECCIÓN

Intersección de los conjuntos A y B es el conjunto de elementos "x" que pertenecen a "A" y a "B". Está formado por elementos comunes a los conjuntos que forman la intersección. Se simboliza por A(B y se lee: A intersección B.

Gráficamente, la respuesta es la zona sombreada que contiene a los elementos que pertenecen a ambos conjuntos.

PROPIEDADES DE LA INTERSECCIÓN DE CONJUNTOS

3. DIFERENCIA

Diferencia entre los conjuntos "A" y "B", es el conjunto de elementos "x" que pertenecen a "A" pero no a "B", se simboliza por "A( B"

Ejemplo:

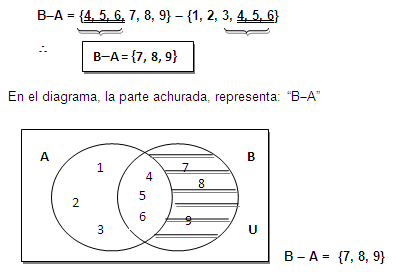
Sean los conjuntos.

A = {1, 2, 3, 4, 5, 6}

B = {4, 5, 6, 7, 8, 9} y el conjunto universal, el conjunto de Números Naturales.

En el diagrama, la parte achurada, representa: "A(B"

A( B = {1, 2, 3}

a. Si el conjunto universal, esta formado por los números naturales la diferencia será:

4. COMPLEMENTACIÓN

Complemento de un subconjunto cualquiera "B" respecto a "U" (conjunto universal), es el conjunto de elementos de "U" que no pertenecen a "B". Se llama también complemento de "B" en "U", o simplemente conjunto diferencia de "U( B". Se lo reconoce por:

Definición 2; complemento de un subconjunto cualquiera "B" respecto a un conjunto "A" que no pertenece a "B". se le llama complemento de "B" en "A", o simplemente conjunto diferencia "A(B".

Ejemplo 1:

Si el conjunto universal está formado por los habitantes de nuestro país, y si "A" es el conjunto de habitantes de nuestra ciudad, entonces "A" representa a los habitantes de nuestro país que no son de nuestra ciudad.

Ejemplo 2:

5. DIFERENCIA SIMÉTRICA

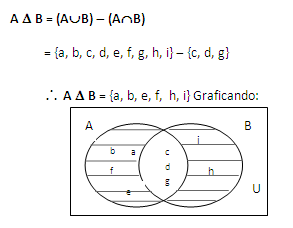
Diferencia simétrica de los conjuntos "A" y "B", es el conjunto de elementos de "A" y de "B", excepto los que pertenecen a la intersección. Esto es, que pertenecen a "A" o "B".